Enfoque Causal o Estadistico.
En el mundo del Aprendizaje Automatico hay un area de mi interes. Se llama Inferencia Causal.
Intentemos entre todos entender, que es la "CAUSALIDAD". Y para eso no creo que se me ocurra mejor idea que casos practicos y reales, por ejemplo: en el ambito de la investigacion forense es normal para los profesionales hablar de causa y efecto.
- Un Medico Forense (Legista), cuando describe una lesion tambien indica en su informe que "elemento" pudo haber causado esa lesion en base al efecto que observa sobre la lesion.
- Un Accidentologo, cuando analiza deformaciones sobre la estructura de un automovil en su informe, toma en consideracion que fuerza fue la necesaria para causar esa deformacion.
- Un Fiscal cuando acusa, relaciona un motivo con un resultado, fundamentando que el motivo causo el resultado que se intenta asociar a una persona.
Y asi podriamos seguir hablando de la relacion Causa-Efecto. Pero detengamonos un momento y veamos que tambien hay otras teorias. Como la de David Hume (Filosofo del siglo XVIII).
Quien indicaba que la relacion causa-efecto no era algo cierto, sino mas bien que ciertos acontecimientos del mundo estan "relacionados" entre si. Y versaba algo asi como "...de hecho, lo unico que encontramos es que un acontecimiento sigue a otro...La mente no siente ningun sentimiento o impresion interna de esta sucesion de hechos."
Entonces para salirnos de la filosofia...cosa que realmente no es mi fuerte. Podemos extraer de esa informacion. Que exsiste al menos una "asociacion" entre distintos elementos para generar un hecho. Lo que nos permite intentar establecer o al menos aproximarnos a entender si uno produce o causa el otro. Y las redes neuronales artificiales entrenadas de forma "supervisada", son un buen elemento para comenzar ya que en ellas lo que se intenta encontrar es una relacion entre los datos de entrada con los datos de salida. Lo que se traduce en encontrar aquellos algoritmos que realmente muestran que datos de entrada predicen la salida y ahi es donde se pone de manifiesto la "asociacion" de la que venimos hablando.
Bien!, cabria a aprtir de aqui la siguiente pregunta. Como encontramos esos algoritmos que nos ayuden a asociar de forma certera los datos de entrada con los de salida?
Y la respuesta que puedo darte es: Mediante las INTERVENCIONES es decir mediante ensayos controlados y aleatorizados, de forma tal de evitar las variables CONFUSORAS.
Variables Confusoras: son aquellas que generan relaciones espurias entre las variables, que intentamos relacionar. Es decir que nos hace creer que las variables estan relacionadas entre si, cuando la realidad es que hay una o mas variables confusoras que las relacionan y no de forma directa entre ellas como creemos.
Vamos a ver un ejemplo claro, o al menos eso espero.
Tomemos las Finanzas y ampliemos nuestro campo de conocimiento o nuestra mente a la forma en que el mercado de valores (la bolsa) trabaja diariamente.
- Todos los dias habiles se operan acciones de empresas (se compran y venden)
- Esta compra y venta genera que el precio suba o baje.
- Sube cuando hay mas compradores que vendedores y baja en caso contrario.
- Este intercambio genera volumen en el mercado es decir un monto de acciones comerciadas.
Entonces si llevamos bien la cuenta aqui ya tenemos 2 variables PRECIO y VOLUMEN. Podriamos preguntarnos si nos conviene comprar cuando el precio baja y vender cuando el precio sube. Seria lo mas logico verdad?.
El problema surge conocer "cuando" esto ocurrira. (Si lo supieramos todos seriamos ricos)
Pero... Si estan relacionados el precio y el volumen entonces podria realmente conocer cuando el precio suba o baje?. Vamos a probarlo.
Primero descarguemos los datos de una accion mensual para que notemos bien el concepto. Vamos a hacer uso de python, la API de alphavantage para descargar los datos y de pandas para crear el dataframe que despues vamos a trabajar.
Elegimos como objetivo la accion de MERCADO LIBRE. (MELI)
import pandas as pd
from alpha_vantage.timeseries import TimeSeries
try:
df = pd.read_csv('./tu_archivo.csv', index_col=0)
print("DataFrame cargado desde el archivo CSV.")
except FileNotFoundError:
print("Archivo CSV no encontrado. Solicitando datos a la API...")
ts = TimeSeries(key="Tu-API-Key", output_format='pandas')
data, meta_data = ts.get_daily(symbol='MELI', outputsize='full')
df = pd.DataFrame(data)
df.to_csv('./nuevo_archivo.csv')
print("DataFrame guardado en el archivo CSV.")Si ahora queremos ver el contenido de lo que acabamos de almacenar tenemos:
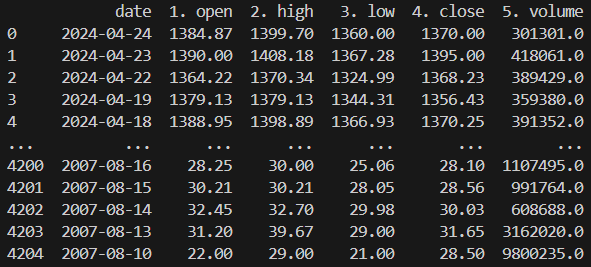
Pero tambien le pedimos los metadatos asique veamos que nos trajo:

Entonces en resumen tenemos los precios diarios de Mercado Libre en Bolsa, el volumen operado, datos relativos a la cantidad de informacion y la zona horaria.
A continuacion lo que hice fue hacer una grafica de los dias del mes de marzo de 2024 y graficarlos.
Tambien los numere y les di color verde si son dias donde el precio subio o rojo si son dias donde el precio bajo. A los fines de darte una mejor vision de la pregunta a responder.
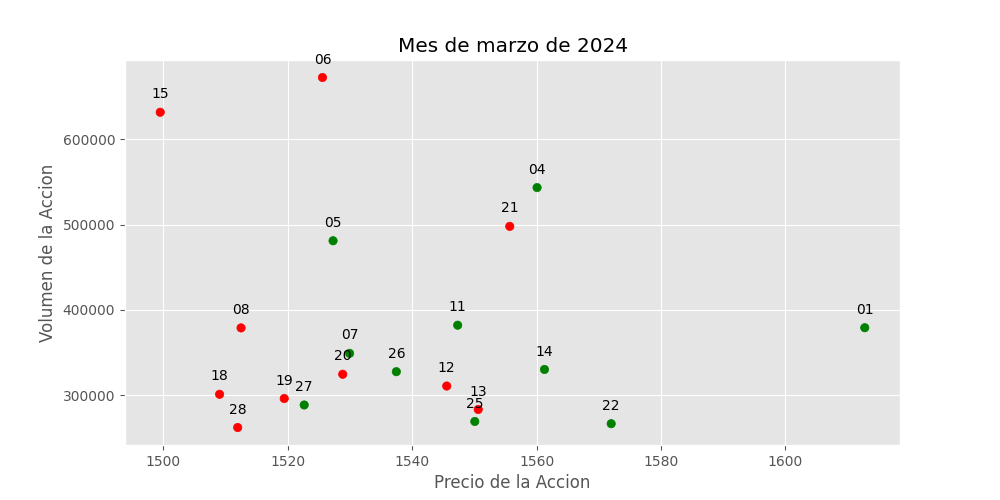
Ahora con esto a la vista me podrias decir si podemos inferir causalmente la relacion entre estas 2 variables? Pensalo un momento y despues segui.
Si te pongo lado a lado ambas variables pero en los ejes x e y opuestos, te ayuda?
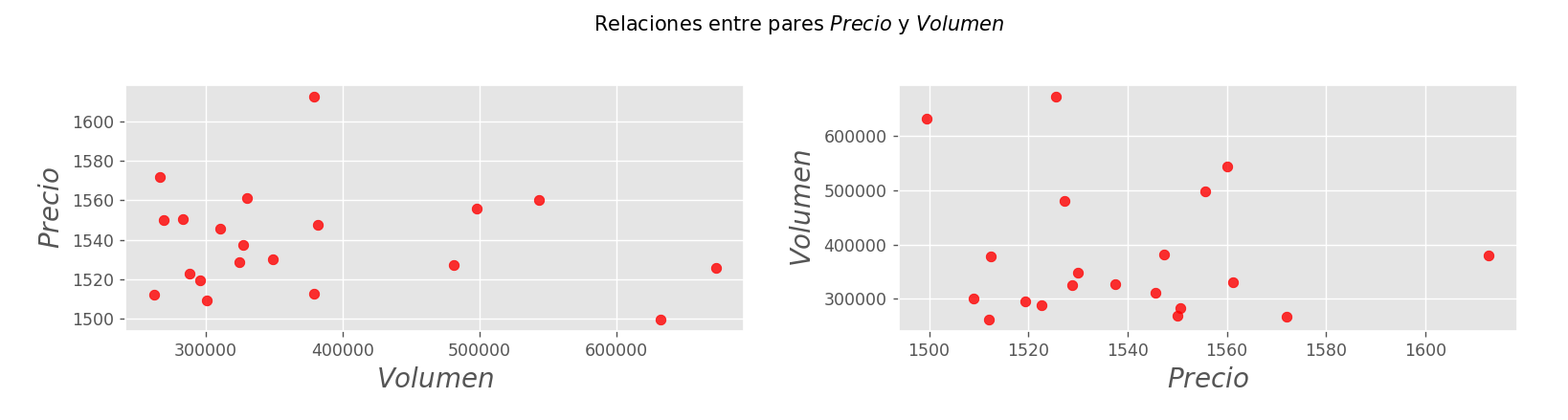
Esto muestra claramente que NO hay relacion lineal o directa entre ambas variables, es decir el volumen NO condiciona el precio y el precio NO condiciona el volumen. A las claras esta que no hay relacion causal o mejor dicho no podemos inferir causalmente una en base a la otra de forma lineal. Es decir son independientes entre si y su realacion es ESPURIA.
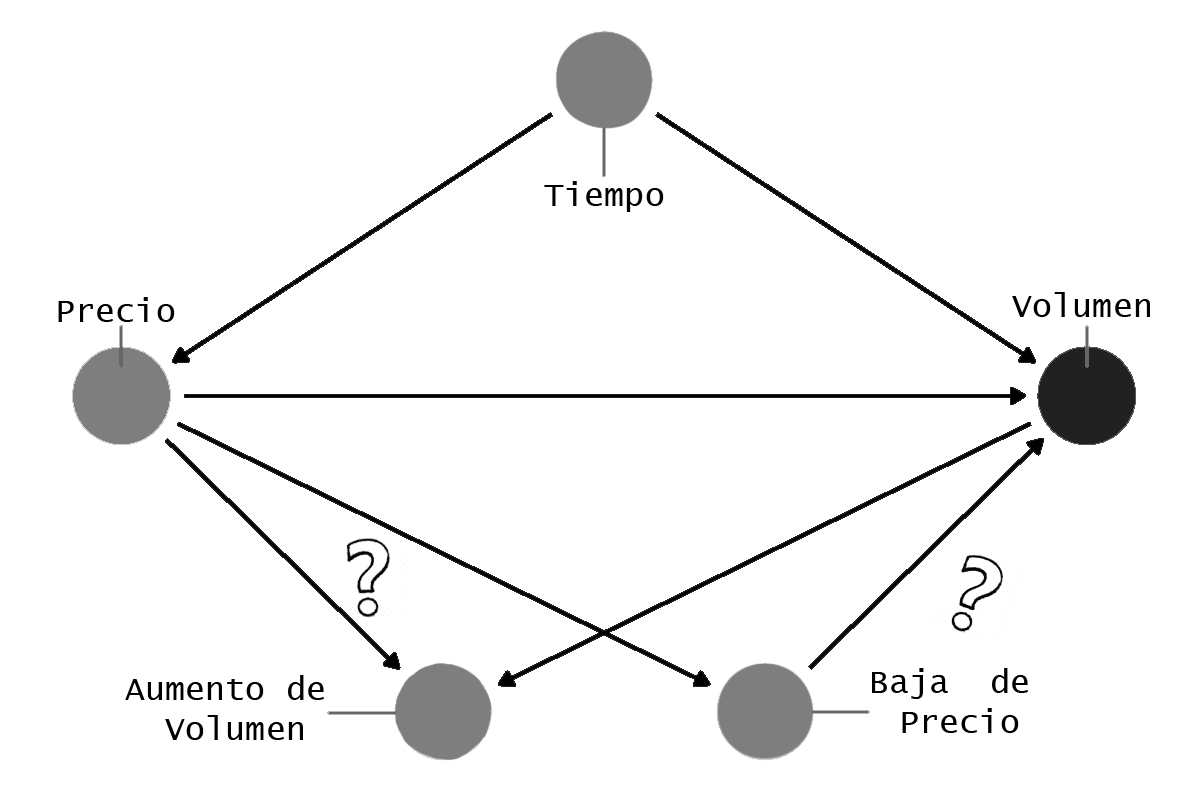
Pero tambien me da otra INFORMACION que es mucho mas importante! Existe 1 o + variables confusoras aqui. Entonces es nuestro trabajo descubrirlas en base a los datos.
Sin embargo aca todavia no te conte de la paradoja de Simpson o efecto Yule-Simpson. Esta paradoja introduce la idea de que una "tendencia" en los datos, desaparece cuando se combina con otros datos incluso aparece la tendencia contraria.
En este caso eso ocurriria si por ejemplo agregaramos otra variable que permita cambiar el conocimiento hasta aqui adquirido. Es decir si agregamos por ejemplo la variable "tiempo". Entonces aparece una relacion entre precio y volumen que hasta el momento desconocemos y si esto resulta real. Entonces la paradoja Simpson se cumple y ademas encontramos nuestra variable confusora.